With the development of our modern cities, growing traffic problems adversely affect people’s traveling convenience more and more, which has become one of the most crucial factors considered in urban planning and design in recent years. Urban traffic congestion is a severe problem that significantly reduces the quality of life in particularly metropolitan areas. However, frequently constructing new roads is not realistic and untenable in social and economic aspects. In the effort to deal with this intractable problem, so-called intelligent transportation systems (ITS) technologies are successfully implemented widely throughout the world nowadays. ITS with two important components advanced traffic management systems (ATMS) and advanced traveler information systems (ATIS) aim to relieve the increasing congestion and decrease travel time through providing information to the drivers by means of radio broadcasts or dynamic route guidance systems.
The provision of accurate real-time information and predictions of traffic states such as traffic flow, travel time, occupancies, etc., is much fundamental and contributive to the great success of ITS (Chen et al., 2010; Dong et al., 2010; Vlahogianni et al., 2004; Lam et al., 2006; Tan et al., 2009; Tang et al., 2003; Thomas et al., 2010; Zhang & Liu, 2008, 2009c). As an important part of ITS, traffic states analysis and traffic forecasting are important in directing commuters to pick optimal routes, which have attracted many researchers to focus on this subject in recent decades. In general, as illustrated in the statement, the traffic forecasting “can be separated into two paradigms: the empirical based, incorporating fairly standard statistical methodology on the one hand, and that based on traffic process theory, either of demand or of supply, on the other” (Van Arem et al., 1997).
Because of the feasibility of data collection from numerous kinds of equipments and the requirements of dynamic management, the empirical approaches for traffic forecasting correspond with the development trends of ITS. It aims to find out the hidden regularity of traffic states through the random and uncertain traffic data by systematic analysis and a variety of mathematics/physics methods.
The empirical approaches can be approximately divided into two types: basic forecasts approaches and combined forecasts approaches. The basic forecasts approach means to predict the traffic state using a certain particular prediction model. The robustness and
accuracy of these approaches lie on the prediction models themselves. Furthermore, basic forecasts approaches can be roughly classified into two types: parametric and nonparametric techniques. Both techniques have shown their own advantages on different occasions in recent years (Tsekeris & Stathopoulos, 2010; Zhang & Liu, 2009f, Zhang & Liu,
2010; Zhang et al., 2010). On the basis of the classification, the chapter provides a systematic review of these models such as historical-mean (HM), filtering algorithm, linear and nonlinear regression, autoregressive process, neural network (NN), fuzzy systems, support vector regression (SVR), and Bayesian networks, etc.
The combined forecasts approach means to combine different forecasts into a single one that is assumed to produce a more accurate forecast. The robustness and accuracy of combined forecast approaches lie not only on the prediction effect of individual prediction model, but also on the efficiency of combination. Because the combined method is to apply each predictor’s unique feature to capture different patterns in the data, it would give a smaller error variance than any of the individual methods (Bates & Granger, 1969). This advantage may make the approach fully scalable to the very large amounts of traffic data practically. Due to its simplicity and practicability, the combined forecasts approach becomes very important to traffic forecasting, and researchers have focused on it, both theoretical and applied.
Though the data-driven traffic forecasting gains many achievements, there still exist some unsolved problems. From the practical point of view, data gained from some detectors are incomplete, i.e., partially or completely missing or substantially contaminated by noises. The missing data sometimes render an entire dataset useless, which is a major hurdle in analyzing traffic information. As missing data treatment is an important preparation step for effective management of ITS, some proper solutions to solve missing data problems are provided in the chapter. And the chapter ends with a brief introdcution of Shanghai Integrated Transportation Information Platform (SITIC), which represents the level of informatization development in transportation.
A brief review of data-driven traffic forecasting
The data-driven traffic forecasting refers to predicting the future state of a certain transportation system based on the historical data, existing traffic data and the related statistics data (Brockwell & Davis, 2002; Chrobok, 2004). Traffic forecasting is a branch of forecasting, and it is an important part of modern transportation planning and intelligent transportation system. Usually, traffic flow, average speed and travel time etc., are defined as the basic parameters of traffic state. Specifically, traffic forecasting is essentially the prediction of these basic parameters based on dynamic road traffic time series data. For instance, most of literature foucs on traffc flow forecasting (Jiang & Adeli, 2004; Qiao et al.,
2001; Abdulhai et al., 1999; Castillo et al., 2008; Chen & Chen, 2007; Dimitriou et al., 2008; Ding et al., 2002; Huang & Sadek, 2009; Ghosh et al., 2005, 2007; Smith et al., 2002), travel time forecasting, and related analysis such as validation, optimization, etc. (Chan et al., 2003; Chan & Lam, 2005; Chang et al., 2010; Kwon, 2000; Kwon & Petty, 2005; Lam, 2008; Lam et al., 2002, 2005, 2008; Lam & Chan, 2004; Lee et al. 2009; Nath et al., 2010; Schadschneider et al., 2005; Tam & Lam, 2009; Tang & Lam, 2001; Yang et al., 2010).
Overall, the process of traffic state variation is a real-time, nonlinear, high dimensional and non-stationary stochastic process. With the shortening of statistical time range, the stochastic and uncertainty of traffic state are more and more strong. Short-term traffic state variation is not only related to the state of the local road section over the past few hours, but also influenced by the traffic states of upstream and downstream road sections, weather situation and unexpected events, etc.
From the spatial and temporal point of view, the traffic state can reflect regular variation. For example, the traffic states of various road sections of urban road network during peak and non-peak period show periodic variation respectively; and the traffic states in urban highway traffic on weekdays and weekends also show different periodic variation, which reflects the temporal regularity of road network traffic. Meanwhile, the urban road network topology, the length of each road link, lane width and traffic direction, etc. can determine the variation of traffic state on a particular road link, which reflects the spatial regularity of road network traffic. Therefore, in the research of transportation prediction, it is essential to fully consider real-time traffic state variation with the randomness and regularity temporally and spatially. Namely, real-time traffic forecasting should predict the future traffic state on the basis of studying the specific sections of the historical traffic data, the whole spatial-temporal road network traffic condition variation, weather situation, and other influence
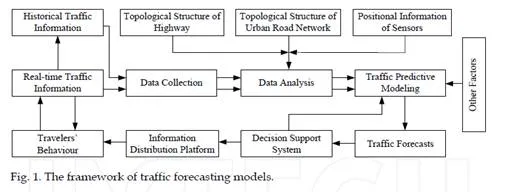
Traffic forecasting approaches
The following factors are usually used for the classification of traffic forecasting approaches: single road link or transportation network, freeways or urban streets, physical models or mathematical methodologies, univariate or multivariate method, etc. From the methodology point of view, the traffic forecasting approaches can be divided into two types: the empirical based approaches and traffic process theory based approaches. For the convenience of data collection from numerous kinds of equipments, a large amount of the historical traffic information and real-time traffic information can be obtained. And the empirical approaches become the new trend of ITS. In this part, we focus on the achievements concerned with empirical approach according to its classification.
Basic forecasts approaches
A large amount of scientific literature has been concerned with basic forecasts approaches. On the basis of the classification, the chapter provides a systematic review of parametric and nonparametric traffic forecasting techniques briefly.
Parametric traffic forecasting approaches
Since the early 1980s, extensive variety of parametric approaches has been employed ranging from historical average algorithms (Smith & Demetsky, 1997; Wu et al., 2004), smoothing techniques (Smith & Demetsky, 1997; Williams et al., 1998), linear and nonlinear regression (Deng et al., 2009; Lu et al., 2009; Zhang & Rice 2003; Sun et al., 2003), filtering techniques (Ross, 1982; Okutani & Stephanedes, 1984; Whittaker et al., 1997; Chien & Kuchipudi, 2003; Stathopoulos & Karlaftis, 2003), to autoregressive linear processes (Min et al., 2010; Min & Wynter, 2011). Thereinto, the autoregressive integrated moving average (ARIMA) (Ahmed & Cook, 1979) family of models such as simple ARIMA (Levin & Tsao, 1980; Nihan & Holmesland, 1980; Hamed et al., 1995; Smith, 1995; Williams, 1999), ATHENA (Kirby et al., 1997), subset ARIMA (Lee & Fambro, 1999), SARIMA family (Smith et al., 2002; Williams et al., 1998, 2003; Ghosh et al., 2005), are classical milestones in forecasting area. Such time series methods belong to time domain approaches, and frequency domain approaches like spectral analysis, “which are regressions on periodic sines and cosines, show their important insights into traffic data which may not apparent in an analysis in the time domain only” (Stathopoulos & Karlaftis, 2001a, b). The parametric traffic forecasting approach is the milestone of the traditional time series forecasting. And it brings significant developments for traffic forecasting.
Nonparametric traffic forecasting approaches
Lately extraordinary development of distinct nonparametric techniques, including nonparametric regression, neural networks, etc., has shown that they may be able to become a high potential alternative to their parametric counterparts (Huisken, 2003; Lam et al.,
2006). In essence, nonparametric statistical regression can be regarded as a dynamic clustering model that relies on the relationship between dependent and independent traffic variables. (Davis & Nihan, 1991; Smith & Demetsky, 1997; You & Kim, 2000; Smith et al.,
2000, 2002; Clark, 2003; Turochy, 2006). In other words, it attempts to identify past information that are similar to the state at prediction time, which leads to easily implemented nature. Over the past decade, another nonparametric technique, artificial neural networks (ANNs) have been applied in traffic forecasting because of their strong ability to capture the indeterministic and complex nonlinearity of time series (Smith & Demetsky, 1994, 1997; Chang & Su, 1995; Dougherty & Cobbet, 1997; Lam & Xu, 2000; Park et al., 1999; Dharia & Adeli, 2003; Wei et al., 2009; Wei & Lee 2007; Lee, 2009). Motivated by the universal approximation property, neural network models ranging from purely static to highly dynamic structures include the multilayer perceptrons (MLPs) (Clark et al., 1993; Vythoulkas, 1993; Lee & Fambro, 1999; Gilmore & Abe, 1995; Ledoux, 1997; Innamaa, 2000; Florio & Mussone, 1996; Yun et al., 1998; Zhang, 2000; Chen et al., 2001), the radial basis function (RBF) ANNs (Lyons et al., 1996; Park et al., 1998; Park & Rilett, 1998; Chen et al., 2001), the time-delayed ANNs (Lingras et al., 2000; Lingras & Mountford, 2001; Yun et al., 1998; Yasdi 1999; Abdulhai et al., 1999; Dia, 2001; Ishak & Alecsandru, 2003), the recurrent ANNs (Dia, 2001; Van Lint et al., 2002, 2005), and the hybrid ANNs (Abdulhai et al., 1999; Chen et al., 2001; Lingras & Mountford, 2001; Park, 2002; Yin et al., 2002; Vlahogianni et al., 2005; Jiang & Adeli, 2005; Quek et al., 2006), etc. Besides the above neural networks models, computational intelligence (CI) techniques that encompass fuzzy systems, machine learning and evolutionary computation have been successfully developed in the field of traffic forecasting. For instance, some literature applies Bayesian networks (Zhang et al. , 2004; Castillo et al., 2008) and Bayesian inference based regression techniques (Khan, 2011; Tebaldi et al., 2002; Sun et al., 2005, 2006; Zheng et al., 2006; Ghosh et al., 2007), some literature uses fuzzy systems or fuzzy NNs to predict the traffic states (Dimitriou et al., 2008; Quek et al., 2009). While others start to explore support vector regression (SVR) to model traffic characteristics and produce prediction of traffic states (Castro-Neto, 2009; Ding et al., 2002; Hong, 2011; Hong et al., 2011; Wu et al., 2004; Vanajakshi & Rilett, 2004). The recent application of different CI techniques and hybrid intelligent systems has shown that the rapidly expanding research field is promising.
Combined forecasts approaches
The basic idea of the combined forecasts approach is to apply each predictor’s unique feature to capture different patterns in the data (Zhang & Liu, 2009d, 2009e). The complement in capturing patterns of data sets is theoretically essential for more accurate prediction (Timmermann, 2005; Huang, 2007). “Both theoretical and empirical findings suggest that combining different methods can be an effective way to improve forecast performances.” (Yu et al., 2005a). The linear combining forecasts methodology has a long historical background. Compared to computational intelligence based nonlinear ensemble forecasting models (Chen & Zhang, 2005; Chen & Chen, 2007), the linear combination retains the conceptual and computational simplicity. In the part, we focus on the application of linear combination method. Researchers have proposed various combined methods since the pioneering work of Bates and Granger. Clemen provided a review and annotated bibliography of the literature for reference (Clemen, 1989). “Research in various fields has strongly suggested that the performance of prediction can be enhanced when (sometimes even in simple fashion) forecasts are combined.” (Yang, 2004).
Basically, we can describe the main problem of combined forecasts as follows. Suppose there are N forecasts such as V P1 (t), V P2 (t), …, V PN (t) (including correlated or uncorrelated
forecasts), where
V Pi (t) represents the forecasting result obtained from the ith model
during the time interval t. The combination of the different forecasts into a single forecast
V P (t) is assumed to produce a more accurate forecast. The general form of such a combined
forecast can be described with formula
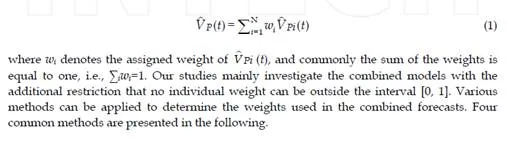
The EW method, applying a simple arithmetic average of the individual forecasts, is a relatively robust method with low computational efforts. Namely, each wi is equal to 1/N (i=1, 2, …, N), where N is the number of forecasts. The beauty of using the simple average is that it is easy to understand and implement, not requiring any estimation of weights or other parameters (Jose & Winkler, 2008). This makes it robust because they are not sensitive to estimation errors, which can sometimes be substantial. It often provides better results than more complicated and sophisticated combining models (Clemen, 1989). Although the approach has non-optimal weights, it may give rise to better results than time-varying weights that are sometimes adversely affected by some unsystematic changes over time. Under the circumstances, the method has the virtues of impartiality, robustness and a good “track-record” in time series forecasting. It has been consistently the choice of many researchers in the combination of forecasts.
Optimal Weights (OW) methods
Bates & Granger proposed that using a MV criterion can determine the weights to adequately apply the additional information hidden in the discarded forecast(s) (Bates & Granger, 1969), and Dickinson extended the method to the combinations of N forecasts (Dickinson, 1973). Assuming that the individual forecast errors are unbiased, we can calculate the vector of weights to minimize the error variance of the combination according to the formula






A brief review of Shanghai integrated transportation information platform
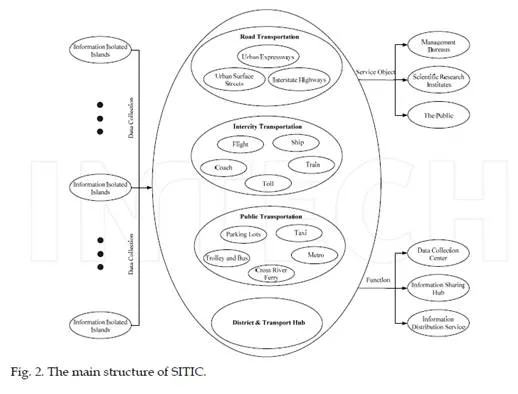
In recent years, we have been exploring traffic informatization and building Shanghai Integrated Transportation Information Platform (SITIC) that provides a mechanism to connect isolated islands of information. After three periods of construction, the system software/hardware, backbone networks, information distribution channels have been completed successfully. The guiding thought for the development of SITIC is “Investigating the present state, revealing the objective laws, and guiding the urban transport more scientifically and efficiently”.
Classifying the transportation into Road Traffic, Public Traffic, Inter-city Traffic and District/Transport Hub, sorts of information of vehicles and people were collected from kinds of sources, which is the basis of the normal running of SITIC and further data mining. Different real-time information on the transportation of Shanghai can be clearly shown in SITIC. Researching the transportation problems in metropolis, especially the traffic prediction, we found that mastering the situation of transportation is important to traffic management, which leads to the essentiality of level division of the road network into macro (network), meso (district), and micro (link) levels. Meanwhile, data gained from some detectors are incomplete, i.e., partially or completely missing or substantially contaminated by noises. This may be caused by malfunctions in data collection and recording systems that often occur in practice. The missing data sometimes render an entire dataset useless, which is a major hurdle in analyzing traffic information. Missing data treatment is another important preparation step for effective management of intelligent transportation systems (ITS). The following figure describes the contents and function of the platform briefly.
Conclusion
The chapter summarizes data driven approaches for traffic prediction in three parts. First, on the basis of classification of the main methods for traffic forecasting, the chapter aims to describe a large amount of literature of traffic forecasting models. And we focus on the decription of combined forecasts approaches that we believe represent the trend of the development of traffic forecasting in practice. Second, from the practical point of view, proper solutions to solve missing data problems are decribled, espertially the state space based approaches. Finally, from the perspective of dynamic traffic management, it presents the corresponding work and experience of traffic informatization in Shanghai.