Effective transportation systems lead to the efficient movement of goods and people, which significantly contribute to the quality of life in every society. In the heart of every economic and social development, there is always a transportation system. Meanwhile, traffic congestion has been increasing worldwide because of increased motorization, urbanization, population growth, and changes in population density. This threatens the social and economic prosperity of communities all over the world. Congestion reduces utilization of the transportation infrastructure and increases travel time, air pollution, and fuel consumption. Therefore, managing and controlling transportation systems becomes a high priority task for every community, as it constitutes a matter of survival and prosperity for humanity.
In the search for meeting the demand for more traffic capacity, it has been realised repeatedly that building more roads is no longer a feasible solution due to the high cost and/or scarcity of land especially in metropolitan areas. In addition, the length of time that it takes to build additional roads and the disruption that this introduces to the rest of the traffic network makes the option of building new roads as the worst case scenario. The current highway transportation system runs almost open loop whereas traffic lights at surface streets are still lacking the intelligence that is necessary to reduce delays and speed up traffic flows. The recent advances in electronics, communications, controls, computers, and sensors provide an opportunity to develop appropriate transportation management policies and strategies in order to effectively utilize the existing infrastructure rather than building new road systems. The use of technologies will help provide accurate traffic data, implement control actions, and in general reduce the level of uncertainty and randomness that exists in today’s transportation networks. The successful implementation of intelligent transportation systems will require a good understanding of the dynamics of traffic on a local as well as global system level and the effect of associated phenomena and disturbances such as shock wave generation and propagation, congestion initiation and so on. In addition, the understanding of human interaction within the transportation system is also crucial.
Transportation systems and traffic phenomena constitute highly complex dynamical problems where simplified mathematical models are not adequate for their analysis. There
is a need for more advanced methods and models in order to analyse the causality, coupling, feedback loops, and chaotic behaviour involved in transportation problem situations. Traffic modelling can facilitate the effective design and control of today’s complex transportation systems. Mathematical models cannot always accurately capture the high complexity and dynamicity of traffic systems. For this reason computer simulation models are developed and tuned to describe the traffic flow characteristics on a given traffic network. Once a computer simulation model is developed and validated using real data, different scenarios and new control strategies can be developed and simulated and evaluated before proposed for an actual implementation.
This chapter presents an overview of traffic flow modelling at the microscopic and macroscopic levels, a review of current traffic simulation software, as well as several methods for managing and controlling the various transportation system modes. In particular, section 2, examines the field of traffic flow theory and the concept of macroscopic vs. microscopic ways of modelling transportation systems. The derivation of traffic flow theory based on the law of conservation of mass, and the relationships between flow speed and density are presented in section 3 under the topic of macroscopic models. Section 4 analyses microscopic car following models and discusses advantages and limitations. Section 5 reviews various some of the most sophisticated traffic software modelling tools, all in relation to intelligent transportation systems. Finally, a summary of recent intelligent transportation systems studies carried out by the authors is provided in section 6 and conclusions are drawn in section 7.
Traffic flow modelling
The study of traffic flow (May, 1990), and in particular vehicular traffic flow, is carried out with the aim of understanding and assisting in the prevention and remedy of traffic congestion problems. The first attempts to develop a mathematical theory for traffic flow date back to the 1930s (Adams, 1937; Greenshields, 1935a), but despite the continuous research activity in the area we do not have yet a satisfactory mathematical theory to describe real traffic flow conditions. This is because traffic phenomena are complex and nonlinear, depending on the interactions of a large number of vehicles. Moreover, vehicles do not interact simply by following the laws of physics, but are also influenced by the psychological reactions of human drivers. As a result we observe chaotic phenomena such as cluster formation and backward propagating shockwaves of vehicle speed/density (Bose
& Ioannou, 2000) that are difficult if at all possible to be accurately described with mathematical models. According to a state of the art report of the Transportation Research Board (Gartner, Messer, & Rathi, 2001), mathematical models for traffic flow may be classified as: Traffic Stream Characteristics Models, Human Factor Models, Car Following Models, Continuum Flow Models, Macroscopic Flow Models, Traffic Impact Models, Unsignalized Intersection Models, Signalized Intersection Models and Traffic Simulation Models. Below we describe briefly each of the above categories.
Traffic stream characteristics (Hall, 1996) theory involves various mathematical models, which have been developed to characterize the relationships among the traffic stream variables of speed, flow, and concentration or density.
Human factor modeling (Koppa, 1999), deals with salient performance aspects of the human element in the context of the human-machine interactive system. These include perception- reaction time, control movement time, responses to: traffic control devices, movement of other vehicles, hazards in the roadway, and how different segments of the population differ in performance. Further, human factors theory deals with the kind of control performance that underlies steering, braking, and speed control. Human factors theory provides the basis for the development of car following models. Car following models (Rothery, 1992), examine the manner in which individual vehicles (and their drivers) follow one another. In general, they are developed from a stimulus-response relationship, where the response of successive drivers in the traffic stream is to accelerate or decelerate in proportion to the magnitude of the stimulus. Car following models recognize that traffic is made up of discrete particles or driver-vehicle units and it is the interactions between these units that determine driver behavior, which affects speed-flow-density patterns. On the other hand, continuum models (Kuhne & Michalopoulos, 1997) are concerned more with the overall statistical behavior of the traffic stream rather than with the interactions between the particles. Following the continuum model paradigm, macroscopic flow models (J. C. Williams, 1997), discard the microscopic view of traffic in terms of individual vehicles or individual system components (such as links or intersections) and adopt instead a macroscopic view of traffic in a network. Macroscopic flow models consider variables such as flow rate, speed of flow, density and ignore individual responses of vehicles. Traffic impact models (Ardekani, Hauer, & Jamei, 1992) deal with traffic safety, fuel consumption and air quality models. Traffic safety models describe the relationship between traffic flow and accident frequency. Unsignalized intersection theory (Troutbeck & Brilon, 1997) deals with gap acceptance theory and the headway distributions used in gap acceptance calculations. Traffic flow at signalized intersections (Rouphail, Tarko, & Li, 1996) deals with the statistical theory of traffic flow, in order to provide estimates of delays and queues at isolated intersections, including the effect of upstream traffic signals. Traffic simulation modeling (Lieberman & Rathi, 1996) deals with the traffic models that are embedded in simulation packages and the procedures that are being used for conducting simulation experiments.
Mathematically the problem of modelling vehicle traffic flow can be solved at two main observation scales: the microscopic and the macroscopic levels. In the microscopic level, every vehicle is considered individually, and therefore for every vehicle we have an equation that is usually an ordinary differential equation (ODE). At a macroscopic level, we use the analogy of fluid dynamics models, where we have a system of partial differential equations, which involves variables such density, speed, and flow rate of traffic stream with respect to time and space.
The microscopic model involves separate units with characteristics such as speed, acceleration, and individual driver-vehicle interaction. Microscopic models may be classified in different types based on the so-called car-following model approach, as it will be discussed in section 4. The car-following modelling approach implies that the driver adjusts his or her acceleration according to the conditions of leading vehicles. In these models, the vehicle position is treated as a continuous function and each vehicle is governed by an ODE that depends on speed and distance of the car in the front. Another type of microscopic model involve the use of Cellular Automata or vehicle hopping models which
differ from the car-following approach in that they are fully discrete time models. They consider the road as a string of cells that are either empty or occupied by one vehicle. One such model is the Stochastic Traffic Cellular Automata (Nagel, 1996; Nagel & Schreckenberg,
1992) model. Further, a more recent approach is currently under heavy research with the use of agent based modeling (Naiem, Reda, El-Beltagy, & El-Khodary, 2010).
Microscopic approaches are generally computationally intense, as each car has an ODE to be solved at each time step, and as the number of cars increases, so does the size of the system to be solved. Analytical mathematical microscopic models are difficult to evaluate but a remedy for this is the use of microscopic computer simulation. In such microscopic traffic models, vehicles are treated as discrete driver-vehicle units moving in a computer-simulated environment.
On the other hand, macroscopic models aim at studying traffic flow using a continuum approach, where it is assumed that the movement of individual vehicles exhibit many of the attributes of fluid motion. As a result, vehicle dynamics are treated as fluid dynamics. This idea provides an advantage since detailed interactions are overlooked, and the model’s characteristics are shifted toward the more important parameters such as flow rate, concentration, or traffic density, and average speed, all being functions of one-dimensional space and time. This class of models is represented by partial differential equations. Modeling vehicular traffic via macroscopic models is achieved using fluid flow theory in a continuum responding to local or non-local influences. The mathematical details of such models are less than those of the microscopic ones. The drawback of macroscopic modeling is the assumption that traffic flow behaves like fluid flow, which is a rather harsh approximation of reality. Vehicles tend to interact among themselves and are sensitive to local traffic disturbances, phenomena that are not captured by macroscopic models. On the other hand, macroscopic models are suitable for studying large-scale problems and are computationally less intense especially after approximating the partial differential equation with a discrete time finite order equation.
There exists also a third level of analysis the so called mesoscopic level, which is somewhere between the microscopic and the macroscopic levels. In a mesoscopic or kinetic scale, which is an intermediate level, we define a function f (t , x , v) , which expresses the probability of
having a vehicle at time t in position x at velocity v . This function, following methods of statistical mechanics, can be computed by solving an integro-differential equation, like the Boltzmann Equation (K. Waldeer, 2006; K. T. Waldeer, 2004).
The choice of the appropriate model depends on the level of detail required and the computing power available. Because of advancements in computer technology in recent years, the trend today is towards utilizing microscopic scale mathematical models, which incorporate human factors and car following models as a driver-vehicle behavior unit.
In the next two sections, macroscopic and microscopic models are examined in more detail.
Macroscopic traffic flow models
Macroscopic flow models (J. Williams, 1996), discard the real view of traffic in terms of individual vehicles or individual system components such as links or intersections and adopt instead a macroscopic fluid view of traffic in a network. In this section, we will cover
the vehicle traffic flow fundamentals for the macroscopic modeling approach. The relationship between density, velocity, and flow is also presented. Then we derive the equation of conservation of vehicles, which is the main governing equation for scalar macroscopic traffic flow models. The macroscopic models for traffic flow, whether they are one-equation or a system of equations, are based on the physical principle of conservation. When physical quantities remain the same during some process, these quantities are said to be conserved. Putting this principle into a mathematical representation, it becomes possible to predict the density and velocity patterns at a future time.
![]() Drawing an analogy between vehicle dynamics and fluid dynamics (Kuhne & Michalopoulos, 1997) let us consider a unidirectional continuous road section with two counting stations 1, 2 at positions x and x . The spacing between stations is x . In such a
Drawing an analogy between vehicle dynamics and fluid dynamics (Kuhne & Michalopoulos, 1997) let us consider a unidirectional continuous road section with two counting stations 1, 2 at positions x and x . The spacing between stations is x . In such a
1
case, the number of cars in a segment of a highway x is a physical quantity, and the process is to keep it fixed so that the number of cars coming in equals the number of cars going out of the segment.
As it will be shown there is a close interrelationship between three traffic variables that is density, velocity and traffic flow. Suppose that in the above scenario, cars are moving with constant velocity v , and constant density such that the distance d between the cars is also constant. Let an observer measure the number of cars N per unit time t that pass him/her (i.e. the traffic flow q ).





phenomena with considerable accuracy, their main limitations arise in their inability to accurately simulate severe traffic congestion situations, where the conservation equation does not represent the traffic flow so well.
On the other hand, it is desirable to use macroscopic models if a good model can be found that satisfactorily describes the traffic flow for the particular traffic problem situation. The advantage of macroscopic models is their flexibility since detailed interactions are overlooked, and the model’s characteristics are shifted toward important parameters such as flow rate, concentration or traffic density, and average speed. If the transportation/traffic problem demands more detail and accuracy such as the case of evaluating the effects of closely spaced intersections or bus priority systems on the traffic network then one should resort to microscopic models, which are described in the next section.
Microscopic driver-vehicle behaviour models
In this section well known car-following microscopic traffic flow models are presented and evaluated on their capability to realistically model traffic flow at the vehicle level.
In order to derive a one-dimensional simple car following model we first assume that cars do not pass each other. Then the idea is that a car in one-dimension can move and accelerate forward based on two parameters; the headway distance between the current car and the leading car, and their speed difference. Hence, it is called following, since a car from behind follows the one in the front.
Car-following models are based on the assumption that a stimulus response relationship exists that describes the control process of a driver-vehicle unit. This concept is expressed with the stimulus response equation where response is proportionally analogous to a stimulus based on a certain proportionality factor (Rothery, 1992) .
As seen later on in this section the various car following models incorporate a variant of the following stimulus response equation.

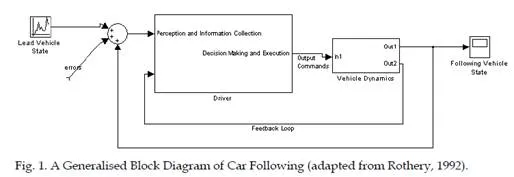
The car-following behaviour is basically, a human interactive process where the driver of the vehicle attempts to reach a stable situation and maintain it by following a leading vehicle, by continuously taking corrective actions like accelerating or decelerating. As it will be seen in the next paragraphs car following models may be classified as Stimulus-Response models, safety distance or collision avoidance models, psychophysical or action point models, and fuzzy logic models. Some of the most widely applied car following models are presented below.
Pipes (Pipes, 1967) proposed a theory of car following behaviour based on what he referred to as the ”idealized law of separation”. The law specifies that each vehicle must maintain a certain prescribed “following distance” from the preceding vehicle. This distance is the sum of a distance proportional to the velocity of the following vehicle and a certain given minimum distance of separation when the vehicles are at rest. Such a model implies that the actions of the following vehicle are only affected by the relative speed between the leading vehicle and the following vehicle. Forbes (Forbes, 1963) modelled car following behaviour by assuming that drivers choose to keep a minimum time gap from the rear end of leading vehicle. The Forbes model of car following also implies that the actions of the following vehicle are only affected by the relative speed between the leading vehicle and the following vehicle.
The General Motors Research Laboratories published significant amount of work on the car- following theory model in a series of papers (Gazis, Herman, & Potts, 1959; Herman, Montroll, Potts, & Rothery, 1959). The basic idea used here is that the actions of the following vehicle in terms of acceleration or deceleration are a function of a single stimulus and the sensitivity of the following vehicle to the stimulus under the prevailing conditions. The stimulus is assumed to be the relative speed between leading and the following vehicle. Sensitivity to the stimulus is assumed to be affected by the distance headway between the leading vehicle and the following vehicle as well as the speed of following vehicle.
Other approaches such as those by Rockwell et al (Rockwell, Ernest, & Hanken, 1968) present a regression based car-following model, which takes into consideration two leading vehicles, and Chakroborty and Kikuchi (Kikuchi, Chakroborty, & Engineering, 1992) a Fuzzy Inference based car-following model.
Consolidating the various approaches of car following models it can be concluded that the general assumption about the interaction between a leader and follower car is governed by the following equation (Rothery, 1992).



Even though there were many efforts through the years to develop realistic models of car following behaviour there are significant limitations concerning their validity. Limitations arise mainly from unrealistic assumptions about the ability of drivers of following vehicles to perceive relative or absolute speeds and accelerations of the interacting vehicles. As Boer (Boer, 1999) suggests factors such as aging impairment and disability further influence driver reactions, which current car following models do not take into consideration. Further, unrealistic is the assumption that driver behaviour is influenced only by the immediate leading vehicle motion as observed by a number of researchers such as Fox and Lehman, and Bexelius. Also the assumption for an empirical relationship fails to explain actual behaviour as pointed out by (Van Winsum, 1999) and (Gipps, 1981) . Finally, existing car following models are rather idealistic as they assume symmetrical driver responses to traffic stimuli, which is clearly unrealistic as revealed by (Chakroborty & Kikuchi, 1999).
As (Brackstone & McDonald, 1999) conclude in their review on microscopic car following models there are potential pitfalls awaiting the unwary in the use of microcopic models. A comprehensive review on the weaknesses and potential developments of microscopic models is given by (Brackstone & McDonald, 1999).
Research on the existing models of driver behaviour has been restricted to modelling driver behaviour under car-following situations. Little work was found, on models of driver behaviour under various other driving situations. It can be said that most research so far has been concentrated on modelling driver behaviour in situations, where only longitudinal interactions affect the driver. Situations where, either lateral interactions alone or lateral as well as longitudinal interactions affect driver’s behaviour received much less attention.
Microscopic traffic modelling software tools
Microscopic simulation is a term used in traffic modelling and is typified by software packages such as VISSIM (Fellendorf & Vortisch, 2001; Gomes, May, & Horowitz, 2004; Park, Won, & Yun, 2006; PTV, 2005), CORSIM (Lin, 1998; Prevedouros & Wang, 1999; Zhang, McHale, & Zhang, 2003), and PARAMICS (Gardes, 2006; Jacob & Abdulhai, 2006; Ozbay, Bartin, Mudigonda, & Board, 2006). Traffic simulation microscopic models simulate the behaviour of individual vehicles within a predefined road network and are used to predict the likely impact of changes in traffic patterns resulting from proposed commercial developments or road schemes. They are aiming to facilitate transportation consultants, municipalities, government transportation authorities and public transportation companies. The traffic flow models used are discrete, stochastic, time step based microscopic models, with driver-vehicle units as single entities.
Traffic simulation software modelers combine in a single package multiple traffic flow mathematical models and therefore make it possible to combine the current knowledge on traffic theory when analyzing a traffic congestion problem. A screenshot of the VISSIM graphical user interface is provided in figure 2. The microscopic model depicted in the figure was developed in order to analyze traffic and evaluate the impact of various bus priority scenarios for a traffic network in Nicosia, Cyprus (G. Papageorgiou, 2006; G. Papageorgiou, Damianou, Pitsillides, Aphames, & Ioannou, 2006).
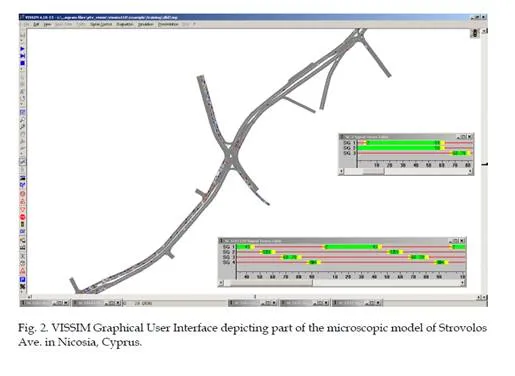
In today’s traffic simulation software, data such as network definition of roads and tracks, technical vehicle and behavioural driver specifications, car volumes and paths can be inserted in graphical user interface mode. Values for acceleration, maximum speed and desired speed distributions can be configured by the user to reflect local traffic conditions. Various vehicles types can also be defined. Further, traffic control strategies and algorithms may be defined as well as interfaces may be built with well-known urban traffic controllers. CORSIM, PARAMICS, VISSIM, and AIMSUN were calibrated and validated in a number of traffic studies worldwide. Below we present some of their main features.
CORSIM which stands for Corridor microscopic simulation is developed by Federal Highway Administration of United States. It has evolved from two separate traffic simulation programs NETSIM and FRESIM. NETSIM models arterials with signalised and unsignalised intersections, while FRESIM models uninterrupted freeways and urban highways.
In the case of VISSIM the microscopic model consists of a psycho-physical car following model for longitudinal vehicle movement and a rule-based lane changing algorithm for lateral movements. The model is based on an urban and a freeway model which were developed by Wiedemann from the University of Karlsruhe. VISSIM is especially well known for its signal control module, which uses a vehicle actuated programming language can model almost any traffic control logic. Further, VISSIM scores high on its ability to model public transportation systems.
AIMSUN was developed by TSS in order to simulate urban and interurban traffic networks. It is based on the car-following model of Gibbs . AIMSUN is therefore based on a collision avoidance car-following model. Traffic can be modelled via input flows and turning movements, origin destination matrices, and route choice models.
PARAMICS, which stands for Parallel Microscopic Simulation, comprises of various modules which include a modeller, a processor, an analyser, a monitor, a converter and an estimator. PARAMICS is well known for its visualization graphics and for its ability to model quite a diverse range of traffic scenarios.
A comprehensive review of simulation models of traffic flow was conducted by the Institute for Transport Studies at the University of Leeds as part of the SMARTEST Project which is a collaborative project to develop micro-simulation tools to help solve road traffic management problems. The study compared the capabilities of more than 50 simulation packages. The results are available on the internet at http://www.its. leeds.ac.uk/ projects/smartest. Other significant reviews of traffic simulation software include the work of (Bloomberg & Dale, 2000) who compared Corsim and Vissim as well as the work of (Boxill, Yu, Training, Research, & Center, 2000) who compared the capabilities of Corsim, Aimsun and Paramics. It can be concluded from the various reviews that software modelers that have comparative capabilities include VISSIM, AIMSUN, and PARAMICS.
In a more recent comparative study of microscopic car following behavior, (Panwai & Dia,
2005) evaluate AIMSUN, VISSIM and PARAMICS. They concluded that the accuracy of a
traffic simulation system depends highly on the quality of its traffic flow model at its core, which consists of car following and lane changing models. In the study the car-following behaviour for each simulator was compared to field data obtained from instrumented vehicles travelling on an urban road in Germany. The Error Metric on distance (Manstetten, Krautter, & Schwab, 1997) performance indicator gave substantially better values for AIMSUN than those of VISSIM and PARAMICS. Further, the Root Mean Square Error (RMSE) was substantially less for VISSIM and AIMSUN than the RMSE for PARAMICS. In another paper presented at the 9th TRB Conference on the Application of Transportation Planning Methods Choa et al. (Choa, Milam, & Stanek, 2004) concluded that although CORSIM provides the shortest traffic network setup time , PARAMICS and VISSIM generated simulation results that better matched field observed conditions and traffic engineering principles.
The reason microscopic simulation models are used over other software packages and methods like the Highway Capacity Manual (HCM) is that microscopic simulations allow us to evaluate the effects that different traffic elements have on each other. Being able to evaluate the effects of closely spaced intersections and interchanges on the traffic network or the effects of a bottleneck condition on the surrounding system, can only be achieved by microscopic traffic simulation models. Also, as metropolitan traffic conditions experience congestion over 3 to 4 hour periods, microscopic traffic simulation programs allow us to evaluate the build-up to congested conditions and the recovery of the system at the end of the period. The peak period of congestion is complex and evaluating solutions under these conditions can only be accomplished using microscopic simulation tools.
In the following section, an approach to modelling and simulation of intelligent transportation systems (ITS) is proposed and implemented for a particular case study in Nicosia , Cyprus. The approach utilizes the VISSIM microscopic simulation modeler.
ITS studies using microscopic simulation
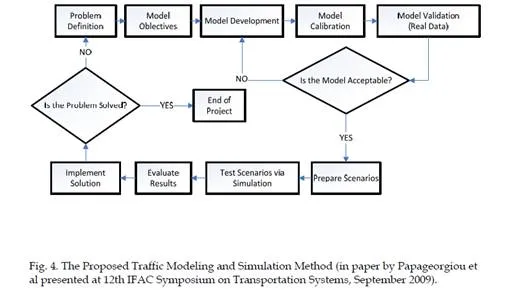
As described in the previous sections traffic phenomena constitute a dynamical problem situation, which makes traffic modeling and simulation a very complex, iterative and tedious process. In order to increase chances for developing a realistic simulation model the following methodology is developed, which is based on the suggestions of (Lieberman & Rathi, 1996) and (Dowling, 2007). This is applied for the modeling of Archangelou Avenue traffic network in Nicosia, Cyprus as described below.
The study area is depicted in figure 3, which shows Archangelou Avenue with its nearby traffic network. Archangelou Avenue is the main road connecting the Rural Nicosia District to the centre of Nicosia, where the main business center is located. Nicosia, the capital of Cyprus, has a population of around 350,000 people. Archangelou Ave., which is one of the three main arterial roads exhibits very high traffic flows as compared with the other regions of metropolitan Nicosia. Further, Archangelou Avenue serves as the connector between Nicosia and a large and heavily populated area of urban and rural communities.
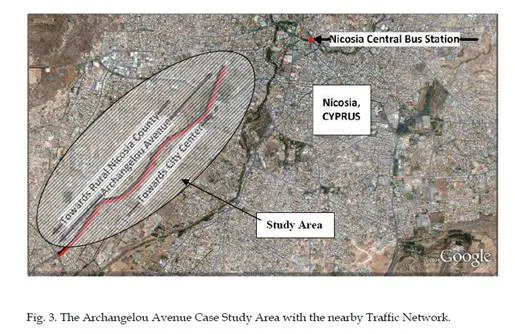
The aim of the study titled “Intelligent Transportation Systems in Archangelou Avenue (BUSSIM)“ was to develop and test BRT strategies via scenario analysis in a computer simulated environment. Scenarios that were evaluated include a number of configurations regarding the introduction of dedicated bus lanes as well as bus advance signal areas as well as High Occupancy Vehicle (HOV) lanes. The scenario analysis was carried out via computer experiments using a microscopic simulation model of Archangelou Avenue urban traffic network. The case study presented in this chapter is part of the BUSSIM research project (George Papageorgiou, Maimaris, Ioannou, Pitsillides, & Afamis, 2010) which was funded by the Cyprus Research Promotion Foundation and Transim Transportation Research Ltd.
As shown in figure 4, the first step of the proposed approach is to identify and define the problem. In our case the symptoms of the problem which are attributed to traffic congestion manifest themselves as increasing travel times for all transport modes. The main causes to the problem of traffic congestion in Nicosia consist of an increasing number of vehicles and a decreasing use of the bus transportation system. Adding more capacity to the road infrastructure will only make things worse, as a reinforcing feedback loop is created where further use of private vehicles is encouraged and use of the public transport is discouraged. Therefore, the long term solution to the problem is to balance or even to turn around the situation by encouraging the use of the public transport mode.
The model incorporated a significant amount of various traffic data that may be classified in terms of static data and dynamic data. Static data represents the roadway infrastructure. It includes links, which are directional roadway segments with a specified number of lanes, with start and end points as well as optional intermediate points. Further, static data includes connectors between links, which are used to model turnings, lane drops and lane gains, locations and length of transit stops, position of signal heads/stop lines including a reference to the associated signal group, and positions and length of detectors. Dynamic data was also specified for the traffic simulation experiments. It included traffic volumes with vehicle mix for all links entering the network, locations of route decision points with routes, that is the link sequences to be followed, differentiated by time and vehicle classification, priority rules, right-of-way to model un-signalized intersections, permissive turns at signalized junctions and yellow boxes or keep-clear-areas, locations of stop signs, public transport routing, departure times and dwell times.
Having introduced the necessary traffic parameters in the model, the iterative process begun, which consisted of model development calibration and validation of the model.
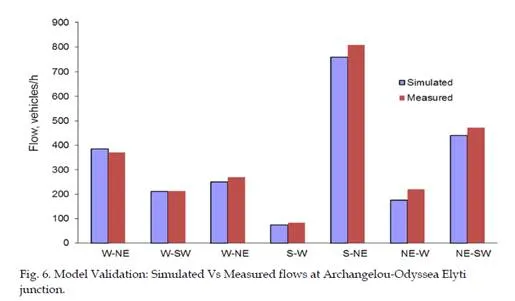
Figure 6 shows the real Vs simulated traffic flows of the various vehicle movement directions of a central intersection of Archangelou Avenue, in particular that of Archangelou-Odyssea Elyti. As seen in the bar chart, traffic flows of real measurements obtained and those of simulated results, are quite comparable. In particular the error ranges from only 1% to 5%, a fact that contributes to building confidence for the model. Further, the simulation model demonstrated the queues that are encountered in reality during the morning peak hours.
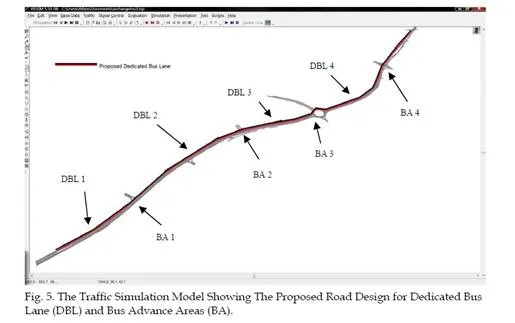
With a validated model in our hands, next comes the preparation of BRT scenarios, their evaluation and the analysis of the results. After consultations with the transportation planning section of the Ministry of Communications Works we came up with several plausible scenarios. In summary, the various scenarios involve the use of dedicated bus lanes and High Occupancy Vehicle lanes by means of Intelligent Transportation Systems.
Even though the modelling process and especially the calibration of the microscopic model was time consuming, results from the simulation experiments gave us significant information on a variety of measures of effectiveness (MoE). In particular, we have managed to compute travel times, queue lengths, delays, average speeds, lane changes and other MoEs for the various scenarios under investigation. On the basis of the various MoEs comparison was carried out between the various scenarios using hypothesis testing with a 95% confidence interval (results submitted for publication). Such valuable information is obviously essential for the implementation of any Intelligent Transportation Systems project.
Conclusion
Modelling and simulation methods are essential elements in the design, operation and control of Intelligent Transportation Systems (ITS). Congestion problems in cities worldwide have drawn a high level of interest for better management and control of transportation systems. Of major importance are ITS systems that include advanced traffic management and control techniques. Such techniques include real-time traffic control measures and real- time traveller information and guidance systems whose purpose is to assist travellers in making departure time, mode and route choice decisions. Transportation research is heading towards developing models and simulators for use in the planning, design and operations and control of such intelligent transportation systems.
This chapter presented an overview of the most important developments in traffic flow theory, and examines modelling of traffic flow at two fundamental levels: the macroscopic level, where traffic is regarded as a fluid, and the microscopic level, where traffic is represented by individual driver-vehicle units. Concerning these two levels of analysis, without discarding the usefulness of macroscopic models it may be concluded that as a result of advancements in computer technology, and the need for more detailed and accurate traffic models there is a trend nowadays for microscopic traffic models where the ultimate goal is to capture the driver-vehicle unit interactions under a variety of driving conditions in a computer simulated environment.
Further, this chapter provided an insight analysis to the world’s most sophisticated traffic simulation modeller software, VISSIM, AIMSUN, CORSIM and PARAMICS, where their capabilities and limitations are discussed. Also, an approach to modeling and simulation of intelligent transportation systems is proposed and implemented. The proposed approach goes through various stages, which include problem identification, model objectives, model development, model calibration, model validation, scenario preparation, simulation experiments and simulated results evaluation. The proposed approach is applied in the case of developing a microscopic traffic simulation model for the urban traffic network of Archangelou Avenue, Nicosia, Cyprus in order to examine alternative bus transport mode enhancements by means of Intelligent Transportation Systems.


Comments are closed